En los últimos años me he mudado más de una vez. Una y otra vez he tenido que medir habitaciones o muebles y luego comprobar si puedo disponerlo todo tal como lo había planeado. Cuando utilizamos una cinta métrica, un metro plegable o una regla, no nos preguntamos si el objeto que estamos midiendo es mensurable. Mientras algo no se extienda infinitamente, deberíamos poder asignarle una longitud, un área o un volumen. Eso es exactamente lo que supusieron los matemáticos, hasta finales del siglo XIX, cuando todo cambió.
Durante mucho tiempo, si querías medir objetos geométricos, procedías como yo cuando me mudaba de casa: sacabas la cinta métrica y listo. Es cierto que si se quería determinar el área debajo de una curva complicada, la tarea se volvía más difícil. Con el Desarrollo del cálculo en el siglo XVII., los matemáticos Isaac Newton y Gottfried Wilhelm Leibniz proporcionaron nuevos instrumentos de medición en forma de integrales y derivadas que podían usarse para determinar con precisión el tamaño de figuras geométricas. Pero durante más de 200 años nadie se preguntó realmente cómo se debían medir los objetos.
A finales del siglo XIX, cuando los expertos intentaron darle a las matemáticas una base estable, la teoría de conjuntos se convirtió en la piedra angular. Esta teoría plantea que todo, incluidas las formas geométricas y las ecuaciones diferenciales complejas, puede rastrearse hasta conjuntos elementales. Pero si las formas geométricas no son más que conjuntos, entonces debemos descubrir cómo medir conjuntos abstractos.
Sobre el apoyo al periodismo científico
Si está disfrutando este artículo, considere apoyar nuestro periodismo galardonado al suscribiéndose. Al comprar una suscripción, ayudas a garantizar el futuro de historias impactantes sobre los descubrimientos y las ideas que dan forma a nuestro mundo actual.
Tomemos el intervalo en la recta numérica entre 0 y 1, que se escribe como [0, 1]. Contiene una cantidad infinita de números reales, pero, para nuestros propósitos, digamos que su longitud corresponde a un centímetro. A los matemáticos les gusta calcular sin unidades y por eso definen que el intervalo [0, 1] tiene la longitud 1. De manera similar, el intervalo [0, 2] tiene una longitud de 2, y así sucesivamente.
Por supuesto, los expertos no decidieron esto simplemente, sino que lo derivaron según ciertas reglas. Para establecer estas reglas intentaron resumir todas las propiedades intuitivas que debe tener una medida como la longitud, el área o el volumen. Es decir, la medida del conjunto vacío debería ser cero; la medida de un objeto no cambia cuando mueves el objeto; y la medida de los objetos que no se superponen es igual a la suma de las medidas de los objetos individuales. A partir de estas tres sencillas conclusiones se pueden definir varias dimensiones, incluida la dimensión de longitud antes mencionada, que corresponde a nuestra intuición.
Para calcular la medida de conjuntos que no se superponen, puede sumar las medidas de los conjuntos individuales.
El procedimiento puede parecer bastante engorroso: al fin y al cabo, conocías el resultado de forma intuitiva. Sin embargo, este enfoque permite medir cantidades de manera más amplia, incluso aquellas para las que no existe una concepción geométrica.
Una medida para cantidades abstractas
Cuando los matemáticos se interesaron por primera vez en las medidas, inicialmente estudiaron funciones (es decir, la expresión o regla que define la relación entre dos variables, X y y). Quizás recuerdes de la escuela secundaria que puedes determinar el área debajo de una función integrándola. Por ejemplo, puedes usar la integral de Riemann, en la que se forman sumas superior e inferior para determinar el área bajo una curva. Vea, por ejemplo, las barras azules en la imagen a continuación, que representan cómo X El eje se puede dividir en pequeños intervalos que se pueden sumar para calcular el área total.
Pero ¿qué pasa si la función es extremadamente complicada? Si nos fijamos en la función de Dirichlet fragmentada, por ejemplo, no se llega muy lejos con el concepto integral habitual. La función de Dirichlet χ(X) tiene el valor 1 si X es un número racional. De lo contrario, el valor de la función es siempre cero. Grafica esta función y verás que χ(X) consta de un número infinito de puntos a lo largo de la recta y = 1 y y = 0. Debido a que la gráfica de la función solo consta de puntos individuales e inconexos, es imposible utilizar la integral de Riemann.
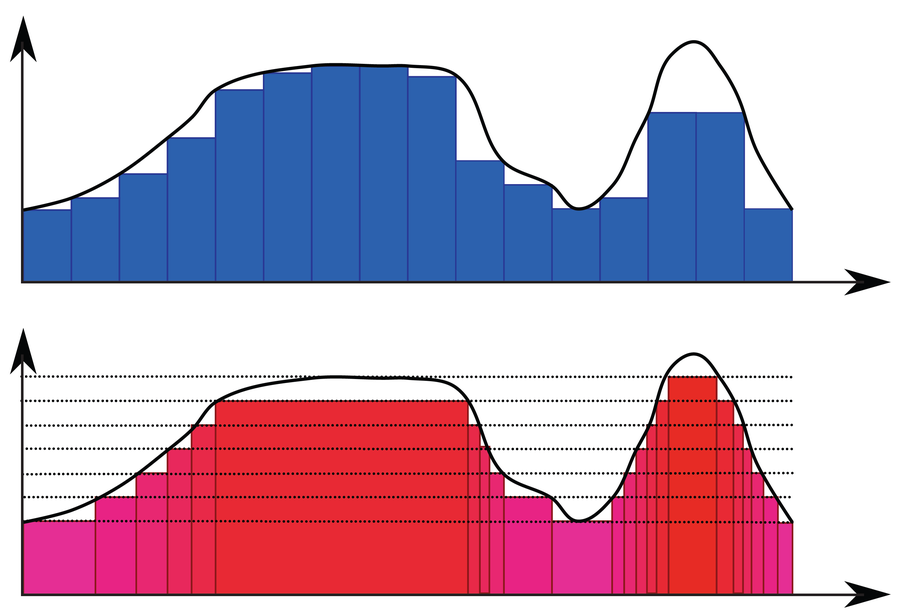
Las integrales de Riemann y Lebesgue definen integrales descomponiéndolas. La integral de Riemann las descompone verticalmente (azul), y Lebesgue los descompone horizontalmente (rojo).
Svebert/Wikimedia Commons (CC0 1.0)
En lugar de ello, es necesario recurrir a la integral de Lebesgue, introducida por matemático Henri Lebesgue en 1902. En este caso, el y El eje se divide en pequeños intervalos, como en las barras rojas de la imagen de arriba. Para calcular un área, debe determinar el ancho de los intervalos correspondientes en el X eje.
Para todas las funciones ordinarias que no están tan fragmentadas como la función de Dirichlet, la integral de Lebesgue y la integral de Riemann proporcionan exactamente el mismo resultado. La ventaja de la integral de Lebesgue es que también puede asignar un área a casos más complicados.
Entonces, para volver a la función de Dirichlet, en el intervalo [0, 1]usemos el intervalo de Lebesgue y dividamos el y eje en pequeñas secciones. Los puntos de la función sólo se encuentran en y = 0 para un irracional X valor o y = 1 para un racional X valor, por lo que el resultado es 0 veces la longitud de todos los números irracionales en el rango [0, 1] más 1 veces la longitud de todos los números racionales en [0, 1]. En este punto, necesitamos la teoría de la medida para asignar una longitud a los conjuntos abstractos: los números irracionales entre [0, 1] y los números racionales entre [0, 1]. Debido a que solo hay una cantidad contable de números racionales (consulte la imagen y el título a continuación para obtener una prueba de esa afirmación), su medida es cero. La medida de los números irracionales restantes entre [0, 1] por lo tanto debe ser 1 (porque todos los números reales en [0, 1] juntos tienen la medida 1). El área debajo de la función de Dirichlet entre cero y uno es, por tanto, 1 x 0 + 0 x 1 = 0.

Considere el conjunto METRO = {metro1, metro2, metro3…, metroi, …}. Porque METRO contiene muchos elementos numerables, se pueden numerar con un índice entero i. Para determinar la dimensión µ(METRO), se puede hacer una estimación. Para hacer esto, forme un pequeño intervalo. Ii alrededor de cada uno metroi con un ancho decreciente y arbitrariamente pequeño ε/(2i): Ii = [mi − ε⁄(2i+1), mi + ε⁄(2i+1)] y formar uno a partir de él nuevo conjunto C = {I1, I2, I3,…, Ii, …}. Entonces C Es similar al conjunto original excepto que no contiene puntos individuales. metro sino intervalos más bien pequeños. En general, la medida de C tendría que ser al menos tan grande como la medida de METRO: µ(METRO) ≤ µ(C). Ahora la medida de C se puede calcular suponiendo que ε se elige tan pequeño que los intervalos Ii nunca se superpongan. La medida corresponde entonces a las longitudes sumadas de los intervalos: μ(C) = ∑i∞ε/(2i) = ε. Esto significa que la medida de METRO debe ser menor o igual a ε: μ(METRO) ≤ ε. Como se puede elegir que ε sea arbitrariamente pequeño, la medida de METRO debe resultar en cero. Esto demuestra que para cada conjunto contable, μ(M) = 0 es válido.
Manon Bischoff/Spektrum der Wissenschaft
Aparece el problema de la medición
La integral de Lebesgue dio origen en 1902 al llamado problema de medición. Los expertos se preguntaban si era posible asignar una medida a cada magnitud. Y apenas tres años después, el matemático Giuseppe Vitali dio una respuesta aleccionadora: no, hay conjuntos que son tan irregulares que no se pueden medir.
Vitali llegó a esta conclusión cuando construyó un conjunto concreto para el que falla cualquier tipo de medida: el conjunto Vitali, que lleva su nombre. Comenzó de manera simple y consideró el conjunto de todos los números entre 0 y 1. Luego dividió este conjunto en diferentes áreas: dos números a y b terminar en el mismo rango si a – b da como resultado un número racional. Por ejemplo, todos los números naturales y todos los números racionales están en la misma región. En otra región, hay 0,2 + √0,2 y 0,3 + √0,2, y así sucesivamente. Vitali dividió así el intervalo [0, 1] en (incontables) infinitas partes pequeñas.
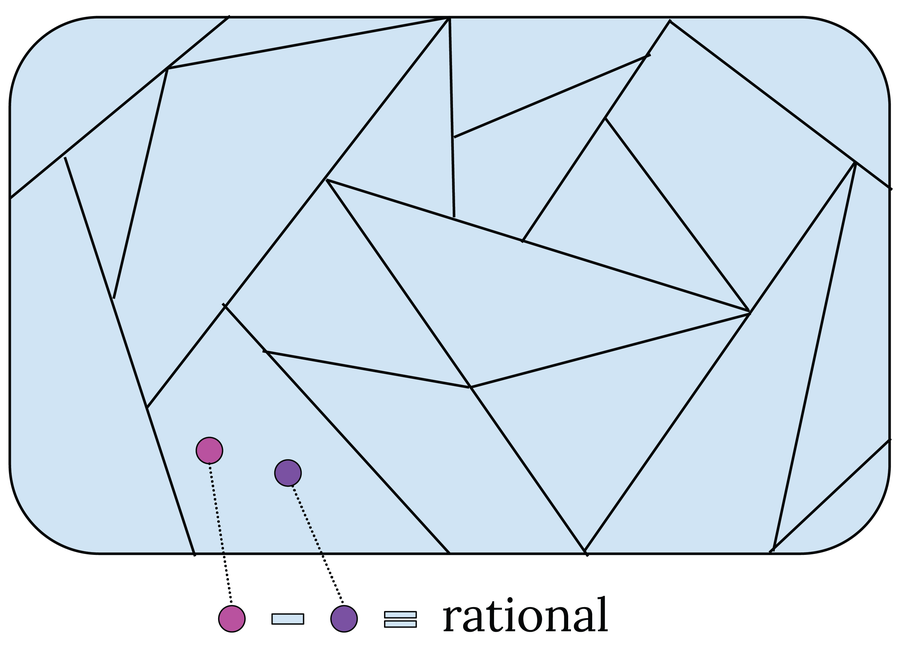
Para construir el conjunto de Vitali, descomponga el intervalo [0, 1] en regiones individuales. Dos números (círculos rosa y morado) están en el mismo rango si su diferencia da como resultado un número racional.
Manon Bischoff/Spektrum der Wissenschaft
En el siguiente paso, seleccionó exactamente un representante. r de cada uno de estos rangos e insertó todos estos representantes en un nuevo conjunto V. El conjunto V contiene así un número incontablemente grande de elementos porque hay un número incontablemente infinito de subdivisiones del intervalo [0, 1]. Entonces Vitali recurrió a un truco: investigó qué sucede si el conjunto V se desplaza en un número racional. pagque asume un valor entre [–1, 1]:vpag =v+ pag. Como resultado, el número racional pag se agrega a cada elemento r en V. De esta manera, Vitali generó un número contablemente infinito de conjuntos Vpag que contienen números entre [–1, 2]. La razón de esto es que V contiene números entre [0, 1] y pag suma valores del intervalo [–1, 1].
Todo esto es bastante técnico, pero no te preocupes; ¡casi estámos allí! El set Vitali V* contiene todos los Vpag y, como veremos, va más allá del concepto de teoría de la medida. Sabemos que la medida de V* es al menos tan grande como la medida del intervalo [0, 1] (porque V* es al menos tan grande como V, que tiene un rango de 0 a 1). Por otro lado, el conjunto de Vitali es menor o igual al intervalo [–1, 2]. Esto significa μ ([0, 1]) = 1 ≤ μ(V*) ≤ μ([–1, 2]) = 3. En consecuencia, el conjunto Vitali debe medir entre 1 y 3.
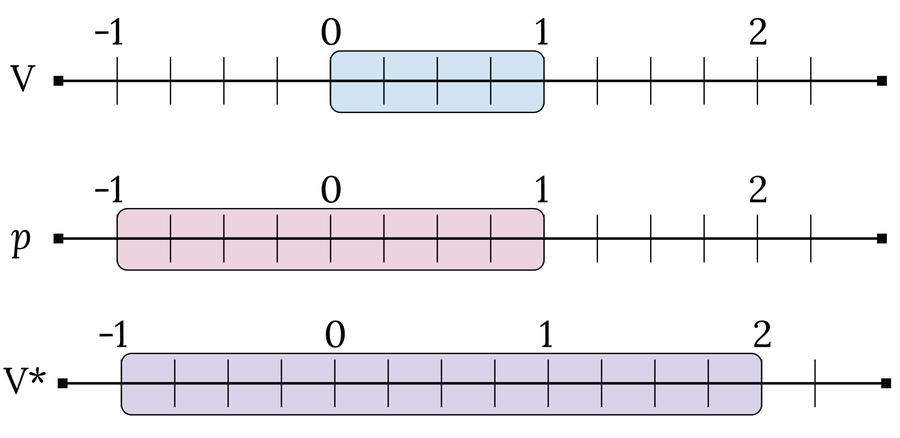
El conjunto V oscila entre 0 y 1, mientras que los valores pag van de –1 a 1. Por lo tanto, el conjunto Vitali V* se extiende de –1 a 2.
Manon Bischoff/Spektrum der Wissenschaft
Ahora también puedes calcular la medida del conjunto Vitali directamente: μ(V*) = ∑pagµ(Vpag) porque sólo hay un número contable pag. El conjunto V.pag contiene un número incontable de elementos entre [p, 1 + p]sin embargo, de modo que μ(Vpag) es un número finito mayor que cero. Y de hecho, todos Vpag son del mismo tamaño: diferentes valores de pag sólo representa un cambio, lo cual es irrelevante para el tamaño de un conjunto. Esto significa μ(Vpag) = µ(V). En consecuencia, la medida del conjunto de Vitali es μ(V*) = ∑pagμ(V), es decir, una constante μ(V) que se suma infinitamente. El resultado de tal cálculo es siempre infinito, independientemente de cuán pequeña sea la constante μ(V). Esto significa: μ(V*) = ∞, lo que contradice la desigualdad anterior 1 ≤ μ(V*) ≤ 3.
Siempre habrá cantidades no mensurables
El sorprendente resultado no significa que hayamos hecho mal los cálculos. Más bien, el conjunto de Vitali es tan complejo que no se le puede asignar ninguna medida. Vitali demostró así que no todas las cantidades son mensurables; También hay cantidades “no mensurables”.
Ese resultado en sí mismo es sorprendente. Al fin y al cabo, el set de Vitali es limitado y sólo contiene valores reales. Si transfieres este resultado a conjuntos bidimensionales, obtendrás resultados aún más extraños: por ejemplo, puedes duplicar el área de superficie de una esfera descomponiéndola en conjuntos no mensurables.
Afortunadamente, las cantidades no mensurables son extremadamente raras. En física, por ejemplo, no ocurren; después de todo, las descomposiciones de los objetos están limitadas por el tamaño de los átomos. Tienes que construir cantidades no mensurables para poder encontrarlas. Y, sin embargo, son omnipresentes: incluso en intervalos numéricos simples acechan secciones no mensurables. Resulta que no es tan fácil deshacerse de tales cantidades. Habría que cambiar los axiomas (y, por tanto, los fundamentos) de las matemáticas. para prevenir la aparición de cantidades no mensurables.
Este artículo apareció originalmente en Spektrum der Wissenschaft y fue reproducido con autorización.

